Bezier Clipping (2)
前回 (BezierClipping(1)) はBezier Clipping法の話に入る前の導入をしました。今日はBezier(ベジエ)曲線について話をしていきます。
みなさんも一生に一回くらいは「滑らかな曲線を描きたいなあ」と思ったことありますよね。実は滑らかな曲線を具体的に表現するのは意外と難しいです。なぜなら、日常生活での滑らかさは美的感覚のことを指すことが多く、その感覚は人によって異なるからです。数学的に滑らかさを表現する方法としては、2階微分までの連続性や、1階微分や2階微分の変化量に制約を与える条件を課すことなどがあります。たとえば、自然3次スプラインと呼ばれる関数では、滑らかさの基準として、
\( \int^{x_n}_{x_1} {f^{\prime \prime} (x) dx} \)
が最小になるように曲線を作ることもあります。このように滑らかな曲線を描くといっても色々な表現があります。
とはいえ「滑らかな曲線を描きたいなあ」と思ったときにはとりあえずCADを起動すると思います。CADでは多くの滑らかな曲線を描くツールが揃っています。そこで、この記事ではAdobeのイラレなどでも採用されているベジエ曲線について説明します。
ベジエ曲線とはなんぞやの話はとりあえずwikipediaを引用したいと思います。
ベジェ曲線(ベジェきょくせん、Bézier Curve)またはベジエ曲線とは、N 個の制御点から得られる N − 1 次曲線である。フランスの自動車メーカー、シトロエン社のド・カステリョ(英語版) とルノー社のピエール・ベジェにより独立に考案された。ド・カステリョの方が先んじていたが、その論文が公知とならなかったためベジェの名が冠されている[1]。コンピューター上で滑らかな曲線を描くのに2次ベジェ曲線 (Quadratic Bézier curve) や3次ベジェ曲線 (Cubic Bézier curve) などが広く利用されている。
ベジェ曲線 (ベジェ曲線 – Wikipedia)
よくわからないので、以下では具体的な数式とグラフで説明していきます。
まず、2次元平面に好きな点を好きな数だけ打ってください。CADなどの多くのソフトでベジエ曲線を表現するときには 3点 ~ 4点 で作成することが多いです。以下説明では \( N \) 点とします。これを制御点と呼びます。スプライン補間などではすべての点を通るので通過点となりますが、ベジエ曲線においては始点と終点を除きこの点を通らないので制御点と呼ばれます。
では、3個の制御点を打った人のベジエ曲線を見ていきましょう。
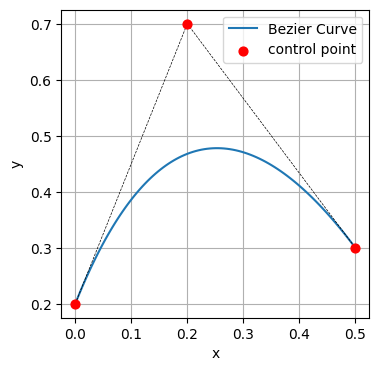
ベジエ曲線では始点と終点は必ず通ります。なので曲線が通らない制御点は \( 3-2=1 \) 点となります。これを点\(A\)と呼ぶことにします。
図をみてわかるように、始点と点 \(A\) を結ぶ線は始点での曲線の接線になっています。また終点と点 \(A\) を結ぶ線は終点での曲線の接線になっています。つまり、この点\( A \) は始点と終点の接線を決める点であるといえます。
次に、4個の制御点を打った欲張りな人のベジエ曲線を見ていきましょう。
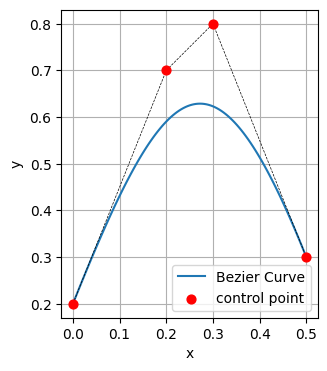
曲線が通らない制御点が\( 4-2=2 \) 点になりました。するとやはり、始点と \( A \) を結ぶ線は始点の接線に、終点と\( B \) を結ぶ線は終点の接線になっていることがわかります。
滑らかな曲線を描きたいと思った時には、入口と出口の接線を作るように点を置けばよいです。そのとき、3個の制御点の場合だとうまく曲線が描けない場合あります。\( 4 \)点の方が入口・出口の接線を自由に設定できます。自由度が高いと呼びます。
このように制御点の位置をうまく調整することで滑らかな曲線を描くことができます。そして、”始点の次の制御点”と”終点の前の制御点”の働きは「曲線の出入口での接線」であることがわかりました。では曲線部はどのようにして作成されるかを見ていきます。
ベジエ曲線を数式で表します。\(N\) 個の制御点を \( b_i \) と置きます。ここで、Pythonのindexが0-であることから, \( (i=0, 1, …, N-1) \) とします。このとき、基底関数 \( J^{n}_{k} (t) \) と実数の媒介変数 \( t \in [0, 1] \) を用いてをベジエ曲線 \( P(t) \) は下記のように書けます。
\( P(t) = \sum_{i=0}^{N-1} b_i \cdot J^{N-1}_{i} (t) \)
この基底関数はバーンスタイン基底関数とよばれ、
\( J^{n}_{k} (t) = {}_n \mathrm{C}_k \cdot t^k (1-t)^{n-k} \)
です。この曲線の意味を考える上でこの基底関数を深堀りしても面白いのですが、ここではあとのBezier Clipping法につながるように、ド・カステリョのアルゴリズムを紹介します。
ド・カステリョのアルゴリズムはベジエ曲線を作図するための方法です。
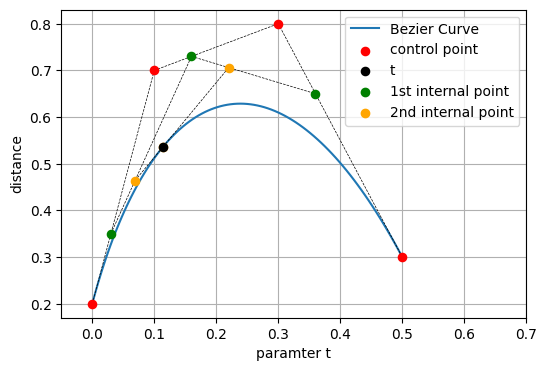
ベジエ曲線は \( t \) を 0 から 1 まで動かして始点から終点までの曲線を作成できます。
このとき、\(t = t_0 \) のときの曲線上の点の位置は下記のようにして作図で求めることができます。
隣同士の制御点 (赤色) を結んで \( t : (1-t) \) に内分した点 (緑色)を書きます。次にその隣り合う内分点 (緑色) を結んだ線分を \( t : (1-t) \) に内分した点 (黄色) を書きます。これを 1 点になるまで繰り返したとき、最後の点が曲線上の点になります。
このアルゴリズムで作った点と先に紹介したベジエ曲線の方程式が一致することを \(N=3\) を例に簡単に手計算して示します。\(b_0, b_1, b_2 \) によって作られる2個の内分点の\( x \)座標はそれぞれ、
\( \left\{ \begin{align*} b^{1}_{0} = (1-t) \cdot b_0 + t\cdot{b_1} \\ b^{1}_{1} = (1-t) \cdot b_1 + t\cdot b_2 \end{align*} \right. \)
ここで右上に内分点が制御点から何世代目かの添え字を書きました。同様にこれらから曲線上の点の \(x\) 座標を計算します。
\( \begin{split} b^2_0 &= (1-t) \cdot b^1_0 + t \cdot b^1_1 \\ &= (1-t) \cdot \{(1-t) \cdot b_0 + t\cdot b_1\} + t \cdot \{ (1-t) \cdot b_1 + t\cdot b_2 \} \\ &= (1-t)^2 b_0 + 2 t (1-t) b_1 + t^2 b_2 \end{split} \)
となってたしかに公式通りになっていることがわかります。
最後にこのベジエ曲線の特徴を紹介しておきます。
まず、\( N \) 個の制御点に対して \( N-1 \) 次元の多項式になることです。これは自由度を上げようとすると次元数も増えることを意味します。一般に高次元の曲線はうねりが生じやすく3次元前後の多項式がよく使われます。すると制御点を4個までしか設定できなくなります。このような課題から使い勝手の良い B-スプライン関数 という発想がでてきます。
次に、ベジエ曲線は常に制御点の凸包の中にあるという重要な性質があります。凸包については次回紹介しますが、Bezier Clipping法の効率性に貢献する重要な性質です。
最後に、ベジエ曲線は任意の箇所で分割でき、その分割後もまたベジエ曲線になります。分割後の制御点の決定法も次回以降に説明します。
これでみなさんも人生において滑らかな曲線に困ったときも描けます。楽しい滑らか曲線ライフを。







ディスカッション
コメント一覧
まだ、コメントがありません